Quelques idées pour développer l’assurance des élèves
| Tout le monde est fait pour les mathématiques | |
|---|---|
| Questions réflexives | Avec l'élève |
| - Qu'est-ce que c'est qu'un élève mathématicien pour moi ? - Comment est-ce que mes explications peuvent favoriser la façon dont les élèves se perçoivent ? - Si on posait la question suivante à mes élèves, quelles seraient leurs réponses ? "D'après vous, à quoi est-ce que j'attribue de l'importance dans votre travail ?" | - Nous sommes tous mathématiciens - Je sais que tu peux y arriver, continue de t'investir. - J'adorerais que tu m'expliques ta façon de traiter ce problème. |
| Tout le monde participe à un voyage mathématiques | |
| - De quelle façon est-ce que mes cours favorisent différentes sortes de résolutions ? - Est-ce que les tâches que je propose permettent aux élèves une résolution différente ? - Est-ce que mes élèves ont l'occasion de partager leur façon de penser ? | - Les élèves ont des expériences différentes sur lesquelles nous nous basons en classe. - Qu'est-ce que tu comprends ? - As-tu encore des questions ? |
| Les erreurs font progresser | |
| - Quelle fonctionnement a été mis en place afin de sécuriser les élèves et qu'ils n'aient pas peur de faire des erreurs - De quelle façon est-ce que les élèves sont mis au défi ? Comment sont accueillies les erreurs ? - Comment est-ce que la correction des travaux d'élèves favorise les opportunités d'apprentissage ? | - Essaie de ne pas gommer tes erreurs car elles peuvent t'apprendre des choses. - Cet élève à beaucoup travaillé, que remarquez-vous ? _ Je demande plusieurs réponses et elles sont toutes écrites au tableau qu'elles soient justes ou fausses. |
| Tout le monde a une expérience et des connaissances riches et intéressantes | |
| - Qu'est-ce que je connais de l'environnement où vivent mes élèves ? - Que font mes élèves à la maison avec leur famille, amis qu'ils pourraient réutiliser en classe ? - Que savent-ils déjà ? | - Que remarques-tu ? Quelle questions te poses-tu ? - Que sais-tu déjà au sujet de ... ? - Qu'aimes-tu faire à la maison avec ta famille ou tes amis ? Arrives-tu à faire des connexions avec ce que l'on voit en classe ? |
| Le raisonnement est plus important que la réponse | |
| - Est-ce que je demande souvent à mes élèves d'expliquer leur raisonnement ? - Quels détails est-ce que je remarque dans les stratégies de mes élèves ? | - Explique moi comment tu as résolu cette tâche. - Cette une façon originale de commencer cette tâche et ta démarche est assez détaillée pour que je comprenne ce que tu as fait. - J'ai fait les groupes en fonction des stratégies utilisées. Dans chaque groupe, j'aimerais que chacun explique sa stratégie. |
Source: adapté de NCTM janvier 2023
Privilégier la représentation multiple des concepts
Source: adapté de NCTM juin 2022
La suite de cette page est fortement inspirée du livre de Margaret Smith et Miriam Gamoran Sherin, The 5 practices in practice, 2019.
Les auteures établissent un tableau des 8 méthodes efficaces d’enseignement des mathématiques.
| Établir des buts clairs afin de focaliser les apprentissages. Afin d'être efficaces, les élèves doivent connaître les buts visés. Les buts doivent être élaborés en suivant le processus d'apprentissage et ceux-ci doivent guider l'enseignement et l'évaluation. |
| Privilégier l'utilisation de tâches qui favorisent le raisonnement et la résolution de tâches complexes. En utilisant des tâches complexes, l'enseignant induit des discussions et des raisonnements riches. Les points d'entrée sont multiples et plusieurs solutions sont parfois possibles. |
| Créer et mettre en évidence des connexions entre différentes représentations. Un enseignement efficace des mathématiques encourage les élèves à faire des liens entre diverses représentations d'un concept. |
| Faciliter les discussions entre les élèves. Afin qu'ils puissent partager une compréhension commune des concepts mathématiques, les élèves seront amenés à comparer leurs méthodes et à argumenter. |
| L'enseignant pose des questions qui nécessitent une bonne dose de réflexion. |
| Baser les automatismes sur la compréhension des concepts sous-jacents. Cela permettra aux élèves de mieux comprendre ce qu'ils font. Ils seront ensuite plus à l'aise pour adapter leurs connaissances à de nouveaux domaines. |
| Proposer et accompagner les tâches difficiles. Un enseignement efficace des mathématiques consiste à proposer aux élèves seuls ou en groupes, des tâches demandant un effort intellectuel en lien avec des concepts utilisés. |
| Récolter et utiliser les preuves de réflexion de vos élèves. Cela permettra de mettre en évidence leurs progrès. Cela vous donnera l'occasion d'adapter vos explications afin de favoriser la compréhension de chaque élève. |
Vue d’ensemble des 5 pratiques qui seront développées dans la suite de cet article :
| Pratiques | Risques de biais selon NCTM n° 115_12 | ||
| Pratiques à mettre en place lors de la planification des leçons. | Pratique 0: Spécifier les objectifs et sélectionner les tâches. Vous spécifiez les objectifs d'apprentissage et vous choisissez des activités à haut niveau intellectuel. | Sélectionner des objectifs et des tâches qui ne font appel qu'à des procédures simples ou calculatoires. Ceci à cause des perceptions faussées de ce que les élèves sont capables de faire. | |
| Pratique 1: Anticiper les réponses des élèves. Vous réfléchissez à la façon dont vous aimeriez que les élèves résolvent la tâche proposée et préparez des questions auxquelles ils vont devoir répondre. | Prédéterminer ce que les élèves sont capables de faire. | ||
| Pratiques mises en place lors de l'enseignement mais qui ont été pensées lors de la planification. | Les élèves travaillent individuellement ou en groupe | Pratique 2: Observer le travail des élèves. Vous observez attentivement le travail des élèves et vous leur posez des questions afin de vous assurer de l'acquisition des concepts. Ainsi vous pouvez les amener à raisonner plus loin. | Écoute sélective. |
| Passer du travail de groupe à la discussion de classe | Pratique 3: Sélectionner la solution d'un élève. Vous sélectionnez le travail d'un élève qui permettra de mettre en évidence les objectifs qui doivent être atteints. | Interrogé très régulièrement le même élève. Discuter uniquement des stratégies fréquentes. |
|
| Pratique 4: Séquencer le travail de l'élève. Vous déterminez l'ordre dans lequel vous donnez les solutions afin de créer un déroulement cohérent de la leçon. | Donner trop d'importance aux solutions correctes. | ||
| Discussion avec toute la classe | Pratique 5: Faire des liens entre les productions d'élèves et les objectifs. Vous établissez des connections entre les solutions des élèves et les objectifs de la leçon. | Exclure des connexions avec des stratégies jugées trop complexes. | |
0: Spécifier les objectifs et sélectionner les tâches
La première étape lors de la panification d’une leçon consiste à préciser les objectifs que les élèves devront atteindre. Le tableau suivant propose deux façons différentes de rédiger un objectif. Qu’est-ce qui est différent ? Est-ce que la différence est importante ?
| Notions | Rédaction A | Rédaction B |
|---|---|---|
| Pente | Les élèves doivent être capables de calculer la pente d'une droite à l'aide de deux points donnés. | Les élèves comprennent que la pente est le quotient du changement vertical divisé par le changement horizontal entre n'importe quel couple de points. |
| Double distributivité | Les élèves doivent effectuer la double distributivité en multipliant le premier avec le premier, le premier avec le second, le second avec le premier et le second avec le second. | Les élèves vont reconnaître que (x+a) et (x+b) sont des facteurs et que chacun peut représenter une dimension d'un rectangle et que le produit de ces facteurs représente l'aire de ce rectangle. Le résultat de cette aire peut être représenté par l'expression algébrique : ax² + ax +bx + ab. Cette représentation algébrique est aussi le résultat de l'application de la distributivité deux fois. (x+a)(x+b) = x(x+b)+a(x+b) = x² +bx + ax + ab |
Les objectifs rédigés à la manière A sont considérés comme des objectifs de performances. Ces objectifs indiquent ce que les élèves seront capables de faire. Par contre les objectifs de la colonne B sont des objectifs d’apprentissage. Les objectifs d’apprentissage décrivent ce que les élèves doivent comprendre des concepts mathématiques.
En général, plus les objectifs sont réfléchis, plus les décisions durant l’enseignement seront prises dans le but d’améliorer la compréhension des élèves (Mills, 2014, p.2). Si nous voulons que les élèves comprennent ce qu’ils font, nous devons spécifier exactement ce que nous voulons qu’ils comprennent. C’est pourquoi les objectifs d’une leçon ne doivent pas uniquement être fixés en terme d’objectifs procéduraux (performance) mais également en termes d’objectifs de compréhension.
Identifier une tâche complexe qui correspond aux objectifs fixés.
Votre prochaine étape lors de la planification de la leçon consiste à sélectionner une tâche qui correspond aux objectifs fixés. La tâche doit avoir une difficulté qui oblige les élèves à montrer leur compréhension d’un sujet. Une tâche est jugée complexe si aucune piste de départ est proposée (schéma). Il ne s’agit pas d’appliquer un algorithme ou une règle simple. Cela signifie que les élèves doivent explorer la tâche, faire des croquis et rechercher des informations. Pour vous aider, posez-vous les questions suivantes :
- Est-ce qu’il existe plusieurs chemins permettant d’entrer dans le problème ?
- Comment l’élève peut-il montrer ses compétences ?
- Est-ce que la tâche nécessite une justification ou une explication ?
- Est-ce que la tâche permet de faire des connexions entre différentes représentations mathématiques ?
- Est-ce que la tâche permet de développer une modélisation, des généralisations, des règles ?
Vous ferez face à plusieurs difficultés lorsque vous devrez définir des objectifs et sélectionner des tâches. En voici quatre en particulier :
| Difficulté | Description |
|---|---|
| Identifier les objectifs d'apprentissage. | Les objectifs doivent se focaliser sur ce que les élèves vont apprendre et pas sur ce qu'ils vont faire. |
| Développer une tâche complexe. | Souvent ces tâches ne sont pas directement disponibles dans les manuels. C'est à l'enseignant de les développer. |
| S'assurer que la tâche permet d'atteindre l'objectif. | Même avec des objectifs bien définis, il arrive que l'enseignant propose des tâches qui ne font pas progresser les élèves. |
| Introduire la tâche afin que tous les élèves se l'approprient. | L'enseignant doit présenter la situation de façon claire mais sans influencer la méthode de résolution. |
1: Anticiper les réponses des élèves
Après avoir défini les objectifs et sélectionné les tâches, il est maintenant nécessaire d’anticiper les réponses de vos élèves. Vous devrez vous plonger dans la tâche et identifier les différentes stratégies que les élèves vont mettre en place. De quelles manières allez-vous répondre à ces stratégies durant votre enseignement ?
| Action | Questions |
|---|---|
| S'approprier le problème | Comment peut-on résoudre la tâche ? |
| Comment l'élève peut-il commencer la tâche ? | |
| Quelles difficultés l'élève va-t-il rencontrer ? | |
| Réfléchir aux réponses à donner aux élèves. | Quelles questions allez-vous poser pour mettre en évidence la façon de penser de l'élève ? |
| Quelles questions vont vous permettre de faire avancer l'élève ? | |
| Comment mettre en évidence la réflexion des élèves ? | Quelles stratégies voulez-vous voir en oeuvre ? |
La première étape consiste à résoudre la tâche complexe en réfléchissant à sa propre approche. Il convient d’y réfléchir globalement puis en détails en analysant les étapes effectuées. Puis considérez les élèves.
- Quelles approches vont-ils utiliser ?
- Quelles sont les différentes représentations qu’ils pourraient faire ?
- Auront-ils besoin d’objets à manipuler ?
- Quels sont les points d’entrée ?
Lors de vos réflexions, gardez en tête les difficultés auxquelles vos élèves pourraient être confrontés.
- Y a t’il une partie de la tâche particulièrement difficile ?
- Où pourraient-ils être bloqués ?
Le seconde étape consiste à préparer vos réponses aux questions des élèves. Cette étape se base sur l’étape précédente et sur les approches que vous avez pu imaginer. L’utilisation de questions avancées permet de faire progresser les élèves. Il s’agit d’utiliser les productions des élèves comme départ de la question. Les questions doivent permettre aux élèves d’aller plus loin en leur demandant de réfléchir à quelque chose à quoi ils n’ont pas encore pensé.
Durant cette phase, vous développerez deux types de questions: les questions pour faire avancer les élèves et les question pour vérifier l’acquisition des objectifs.
Afin de récolter des traces durant l’enseignement, il est pratique de dresser un tableau à 5 colonnes et de se balader dans la classe en prenant des notes.
| Stratégie de résolution | Question pour évaluer les acquis | Question pour faire avancer les élèves | Qui et quoi | Ordre |
|---|---|---|---|---|
| Stratégie 1 | Question a | Question c | ||
| Stratégie 2 | Question b | Question d | ||
| Autre |
Sherin et Van Es (2009) expliquent qu’il est intéressant pour l’enseignant d’arriver à remarquer les apprentissages mathématiques des élèves durant la résolution des tâches. Il s’agit de faire le tri dans la grande quantité d’informations que vous capterez durant une leçon. La table ci-dessus permet de récolter ce genre d’informations. La colonne « Qui » permet de recenser les stratégies utilisées par les élèves.
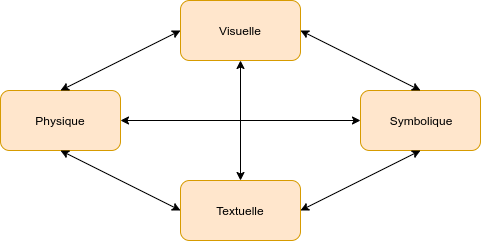
Il est parfois compliqué d’imaginer différents chemins pour résoudre un problème. Une technique consiste à réfléchir aux différentes façons de représenter un problème :
- Visuel (diagramme, graphique, image)
- Algébrique
- Physique (objet)
- Verbal (phrases, texte)
2: Observer le travail des élèves
Après avoir sélectionné minutieusement les objectifs et après avoir réfléchi aux différentes stratégies des élèves, vient maintenant le temps de mettre tout ceci en pratique en classe. Comment conserver une trace de ce que font ou disent les élèves ? Le tableau suivant regroupe quelques questions autours de la récolte de traces :
| Quoi | Questions |
|---|---|
| Suivre la réflexion de l'élève. | Comment allez-vous conserver une trace des réponses de l'élève durant la leçon ? |
| Comment allez-vous vous assurez d'avoir suivi chaque élève ? | |
| Évaluer les réflexions de l'élève. | Est-ce que vos questions vont chercher l'élève là où il est ? |
| Est-ce que vos questions permettent à l'élève de vous montrer où il en est ? | |
| Faire évoluer les réflexions de l'élève. | Est-ce que vos questions sont pilotées par les objectifs que vous avez définis ? |
| Est-ce que les élèves arrivent à répondre à vos questions sans aide ? | |
| Est-ce que vos questions permettent de faire progresser les élèves ? |
En classe soyez à l’affût des stratégies que vous avez anticipées et que les élèves utilisent. Lorsque vous en avez repéré une, vous pouvez alors utiliser les questions que vous avez préparées. Lorsque vous posez une question à un élève, il est important que vous alliez chercher l’élève là où il en est dans sa réflexion. Il sera souvent nécessaire de créer de nouvelles questions en plus de celles préparées.
Une fois que vous avez compris la façon de penser de votre élève, vous pourrez l’aider à avancer. Pour certains élèves cela nécessite de leur demander: « Quel est le but de la tâche ? », « Qu’essayez-vous de faire ? ». Pour d’autres élèves il s’agira de leur demander de considérer des cas spéciaux ou leur demander d’expliquer pourquoi leur approche a fonctionné.
3: Sélectionner la solution d’un élève
Déterminons à présent sur quelles idées et sur quels élèves l’enseignant désire porter son attention lors de la discussion de classe. Il s’agit ensuite d’organiser l’ordre de passage des différents élèves.
| But | Questions à se poser |
|---|---|
| Identifier l'élève dont vous souhaitez mettre le travail en avant. | Quelle stratégie permet à l'enseignant d'accomplir les objectifs qu'il s'est fixé. |
| À quelles difficultés les élèves ont-ils fait face ? Y a-t'il des points communs ? | |
| Sélectionner les élèves qui présentent leur travail. | Quels élèves l'enseignant désire t'il voir présenter ? |
| Comment cette sélection pourrait promouvoir le travail d'un élève ? | |
| Établir une ligne directrice cohérente. | Comment l'enseignant peut-il organiser le travail des élèves afin d'obtenir une séquence cohérente et avec un fil conducteur ? |
4: Séquencer le travail de l’élève
Cette partie consiste à organiser la discussion en classe entière. L’idée ici est de mettre les élèves au centre et de leur demander d’expliquer aux autres leur stratégie. Votre rôle sera de les aider à organiser leurs idées, leur expliquer où se tenir, avec quelle force parler. Il faudra également leur demander d’expliquer la méthode et le raisonnement qu’ils ont utilisés.
5: Faire des liens entre les productions d’élèves et vos objectifs
Afin que les élèves apprennent vraiment ce que vous aviez défini, il est nécessaire que vous mettiez en évidence les liens entre les solutions présentées et les objectifs. Il sera aussi peut-être nécessaire d’expliquer à la classe comment formuler une question, comment montrer son désaccord et comment proposer une solution alternative.
Si vous ne faites pas de liens avec vos objectifs, il y a un risque que vos élèves ne comprennent pas ce qu’ils sont sensés avoir appris lors de l’exercice.
Le tableau suivant vous donne quelques pistes pour impliquer vos élèves dans les discussions :
| Votre action | But | Exemples |
|---|---|---|
| Ajouter: Demander aux élèves de compléter. | Favoriser la participation d'autres élèves afin d'approfondir la compréhension d'une idée. | Quelqu'un aimerait ajouter quelque chose à ce qui a été dit ? Peux-tu en dire plus sur ce que tu as compris ? |
| Raisonner: Demander aux élèves de comparer leur propre résultat avec celui de quelqu'un d'autre. | Permettre aux élèves de donner du sens à ce que leurs camarades expliquent. | Êtes-vous d'accord ou non ? Pourquoi ? Dans quel sens ce qu'il/elle a dit est similaire ou différent de ce que vous pensiez ? |
| Répéter: Demander à un élève de répéter avec ses propres mots ce qu'un camarade a dit. | Donner aux élèves une autre version de ce qu'ils ont entendu et s'assurer qu'ils soient impliqués. | Est-ce que quelqu'un peut répéter avec ses mots ce qui vient d'être dit ? |
| Reformuler: Vous répétez ce qu'un élève a dit et vous vérifiez avec l'élève que vous avez bien compris ce qu'il a dit. | Clarifier ce qu'un élève a dit. Amplifier l'idée importante du discours de l'élève. | Alors tu veux dire que ... Alors voici ce que j'ai compris ... |
| Attendre: Donner du temps aux élèves pour réfléchir à la question que vous leur posez. | Permettre à tous les élèves d'avoir assez de temps pour réfléchir à la question posée. | Prenez une minute pour réfléchir à cette question. Je vais attendre jusqu'à ce que je voie plus de mains levées. Prenez votre temps, j'attends. |
| Douter: Permettre aux élèves de changer leur réponse suite aux discussions précédentes. | Montrer aux élèves qu'il est important de savoir se remettre en question et que c'est ainsi que l'on apprend. | Qui parmi vous aimerait changer d'avis ? Est-ce que l'avis de quelqu'un a changé ? |
| Discussion à deux: Donner du temps aux élèves pour discuter une idée avec leur voisin ou en petits groupes. | Laisser du temps aux élèves pour répondre à une question plutôt que d'attendre une réponse immédiate de leur part. | Prenez deux minutes pour discuter de la question avec votre voisin. |
| Rediriger: Rediriger une question d'élève vers un autre élève. | Renverser la responsabilité du raisonnement vers la classe. Favoriser une compréhension partagée de la discussion. | C'est une bonne question. Que pensez-vous de ce qui vient d'être dit ? |
| Mettre en évidence: Mettre en évidence la contribution d'un élève lors d'une discussion. | Mettre en évidence une contribution qui est directement liée aux objectifs de la leçon. | Est-ce que tout le monde à entendu ce qu'elle vient de dire ? C'est un point important qui vient d'être soulevé ! |
| Résumer: Mettre en avant les points clés d'une discussion. | Permettre à tous les élèves de comprendre ce qu'il est important de comprendre et de savoir faire. | Alors, en repensant à vos présentations, voici ce que je retiens ... Voici ce que nous avons découvert ... |
| Inviter: Demander à un élève de contribuer à la discussion. | Montrer que les points de vues différents sont importants. | .... aimerais-tu partager ce que vous avez fait dans ton groupe ? ...., tu fais une drôle de tête. A quoi penses-tu ? ...., ta stratégie n'était pas la même. Qu'as-tu fait de différent ? |
| Suivre: Rebondir sur les explications d'un élève. | Faciliter la compréhension d'un raisonnement d'élève pour le reste de la classe. | Peux-tu expliquer comment tu as obtenu ... Comment sais-tu cela ? Pourquoi cela fonctionne-t-il ainsi ? |
6: Créer une connexion entre le vocabulaire et les concepts
Il s’agit de créer un diagramme découpé en 4 parties:
Concept: Le mot qui est étudié
Définition: Une définition la plus complète possible
Caractéristiques : Quelques propriétés
Exemples et contre-exemples : Pour illustrer le concept
Quelques stratégies afin de poser des questions à des fins spécifiques
(source: NCTM 113, issue 06, page 454)
| But de la question | Stratégies | Exemples |
|---|---|---|
| Susciter la réflexion | Toujours demander à l'élève comment il a résolu la tâche, que son travail soit juste ou faux. | Comment as-tu trouvé cette réponse ? |
| Reformuler les stratégies en utilisant les mots de l'élève et décrire les actions de l'élève pour confirmer votre compréhension de sa stratégie. | Pourquoi as-tu regroupé ces éléments, quelle logique as-tu utilisée ? | |
| Fournir deux interprétations des paroles ou des actes de l'élève. | As-tu décidé de séparer les poules et les lapins ainsi afin d'avoir deux groupes avec le même nombre d'animaux ? | |
| Générer des idées | Récupérer des informations sur ce que l'élève a compris. | Que te dit la consigne au sujet de .... ? Qu'essaies-tu de faire ? |
| Aider l'élève à comprendre la signification des mots afin qu'il comprenne ce qui lui est demandé. | Que signifie ... ? | |
| Demander à l'élève de dessiner une image afin de démontrer sa compréhension de la tâche. | Peux-tu me montrer à quoi cela ressemblerait avec des multi-cubes ? | |
| Clarifier une explication | Amener l'élève à une contradiction en utilisant des contre-exemples ou des questions "Que se passerait-il si ...". | Que se passerait-il si [changer un paramètre de la consigne] ? |
| Demander à l'élève de tester ses solutions. | Peux-tu relire la consigne en y plaçant ta réponse afin de vérifier si cela a du sens ? | |
| Connecter les stratégies de l'élève avec les actions demandées dans la tâche | À quel endroit dans la donnée, est-il dit de prendre la moitié et où as-tu divisé par deux dans ta solution ? | |
| Justifier une affirmation | Demander pourquoi ou pourquoi pas même si ce que pense l'élève est incorrect. | Pourquoi est-ce que ta solution fonctionne ? |
| Considérer des solutions erronées. | Pourquoi est-ce que cette solution ne fonctionne pas ? | |
| Comparer la stratégie de l'élève à une autre stratégie. | Quelle est la différence entre ta résolution et celle de ton voisin ? |
Quelques situations où une stratégie pédagogique est contre-productive
(source: NCTM 116, issue 04, page 250)
| Cette technique | est productive quand... | est contre-productive quand ... |
|---|---|---|
| Collecter des informations dans la classe. | Vous voulez susciter la réflexion des élèves d'une manière générale. | Vous avez déjà trouvé la contribution d'un élève qui vaut la peine d'être discutée avec toute la classe. |
| Clarifier une explication. | Quelque chose dans les propos d'un élève nécessite une clarification afin que ses camarades s'impliquent et donnent du sens à ce qu'il a dit. | Les propos de l'élève sont assez clairs pour que la classe puisse les utiliser. |
| Demander à un camarade de reformuler. | Vous désirez vous assurer que les élèves ont bien compris le point important de la discussion. | Vous aimeriez apporter un élément nouveau sur lequel vous désirez que les élèves travaillent. |